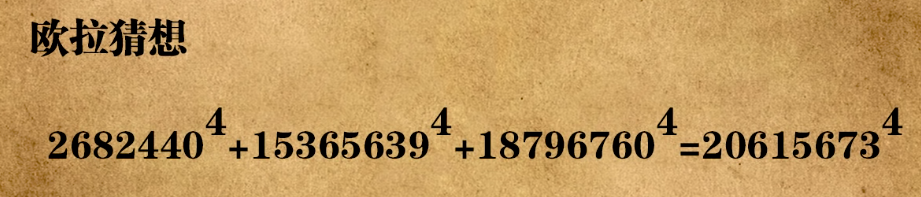费马大定理
费马大定理,也称费马最后定理(法语:Le dernier théorème de Fermat);(英语:Fermat’s Last Theorem),其概要为: \(当整数n>2时,关于 x,y,z的不定方程\\ x^n + y^n = z^n\\ 没有正整数解\)
以上陈述由17世纪法国数学家费马提出,一直被称为“费马猜想”,直到英国数学家安德鲁·怀尔斯(Andrew John Wiles)及其学生理查·泰勒(Richard Taylor)于1995年将他们的证明出版后,才称为“费马大定理”。
证明流程
费马大定理
⇒ 改写成椭圆曲线方程
⇒ 改写成模形式(谷山-志村定理)
数学工具和理论
欧拉的无穷递降法
1770年,欧拉证明n=3时定理成立, 使用了 无穷递降法。无穷递降法,又名无穷递减法,是数学中证明方程无解的一种方法。
这个方法对初中数学计算非常有用。比如
\(\sqrt {2}\)
是无理数的证明。证明方法
谷山-志村定理(英语:Taniyama-Shimura theorem)
志村五郎和谷山丰的理论
谷山-志村定理(英语:Taniyama-Shimura theorem)建立了椭圆曲线(代数几何的对象)和模形式(数论中用到的某种周期性全纯函数)之间的重要联系。


世界上存在5种最基本的计算方法,加减乘除,还有模形式。
伽罗瓦群
伽罗瓦群(法语:Groupe de Galois)是抽象代数中域论的概念,表示与某个类型的域扩张相伴的群,是伽罗瓦理论的基础概念。域扩张源于多项式。通过伽罗瓦群研究域扩张以及多项式的理论,称为伽罗瓦理论,是十九世纪法国数学家埃瓦里斯特·伽罗瓦为了解决“高次多项式方程是否有根式解”的问题而创造的。后世也以他的名字命名相关的概念。
其他
欧拉猜想x
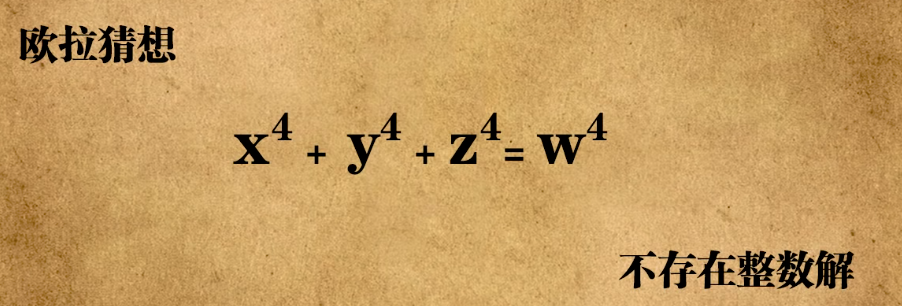
不过可惜命题是错的。。。实际上存在整数解